ESTRUTURAS METÁLICAS E DE MADEIRA
Duas chapas de 204 mm × 12,7 mm (1/2") em aço MR250 (ASTM A36) são emendadas com chapas laterais de 9,53 mm (3/8") e parafusos comuns (A307) com diâmetro de ϕ 25,4 mm (1"). Determinar o esforço resistente Rd relacionado ao corte duplo dos conectores (parafusos).
Rd = 722 kN.
Rd = 767 kN.
Rd = 700 kN.
Rd = 748 kN.
Rd = 793 kN.
Na construção civil brasileira, os principais materiais aplicados com função estrutural são o aço, o concreto e a madeira. Com base nessas informações, e conforme apreciação das propriedades indicadas na tabela abaixo, analise as seguintes afirmativas relacionadas aos três materiais citados:
I. O aço é um material claramente superior à madeira, em diversos aspectos: possui maior durabilidade, maior resistência tanto à tração quanto à compressão, e também é um material naturalmente mais leve.
II. Uma das atribuições do aço quando empregado em estruturas de concreto armado é promover resistência à tração, pois o concreto, em geral, possui baixa resistência à tração.
III. A resistência à compressão do concreto comum geralmente é maior que a resistência à compressão do aço.
IV. A madeira, tanto sujeita à tração quanto à compressão paralela às fibras, possui maior eficiência que o aço e o concreto quando relaciona-se a resistência do material com sua massa específica.
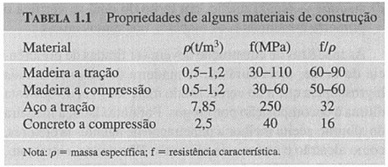
Fonte: PFEIL, Walter; PFEIL, Michèle. Estruturas de madeira: dimensionamento segundo a norma brasileira NBR 7190/97 e critérios das Normas Norte-americanas NDS e Européia EUROCODE 5. Rio de Janeiro: LTC, 2003.
De acordo com a análise efetuada, é possível concluir que as afirmativas CORRETAS são:
I e II
III e IV
II e IV
I e III
I, II e IV
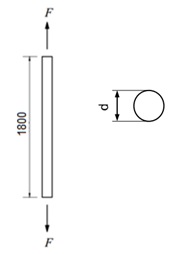
Verificar o diâmetro mínimo, em mm, para a seção transversal circular do tirante de aço MR250 (ASTM A36) ilustrado na figura, sujeito a um esforço normal de tração. No local há elevadas concentrações de pesos fixos. Considerar que o esforço normal de tração é ocasionado pelas seguintes ações:
Peso próprio da estrutura metálica: Ng1 = 32 kN
Peso dos outros componentes não metálicos permanentes: Ng2 = 73 kN
Carga acidental (de ocupação): Nq = 35 kN
Vento: Nv = 20 kN
35 mm.
25 mm.
30 mm.
20 mm.
40 mm.
Determinar o esforço normal resistente de compressão para a coluna soldada (CS) mostrada abaixo, de acordo com a ABNT NBR 8800:2008. As restrições nos dois eixos de análise também são indicadas: a coluna é engastada e livre no eixo X-X, e simplesmente apoiada no eixo Y-Y. Considerar aço MR250 (A36).
Perfil CS 300×62 kg/m:
d = 300 mm
h = 281 mm
tw = 8 mm
tf = 9,5 mm
bf = 300 mm
L = 4000 mm
Nd,res = 1013 kN.
Nd,res = 1447 kN.
Nd,res = 862 kN.
Nd,res = 1976 kN.
Nd,res = 2468 kN.
Em estruturas de aço, as ligações são classificadas conforme o grau de impedimento da rotação relativa das barras conectadas. Na figura abaixo são indicadas algumas ligações de viga e pilar de alma cheia (perfil I ou H) que são frequentemente empregadas na prática, de acordo com a utilização de parafusos e soldas.
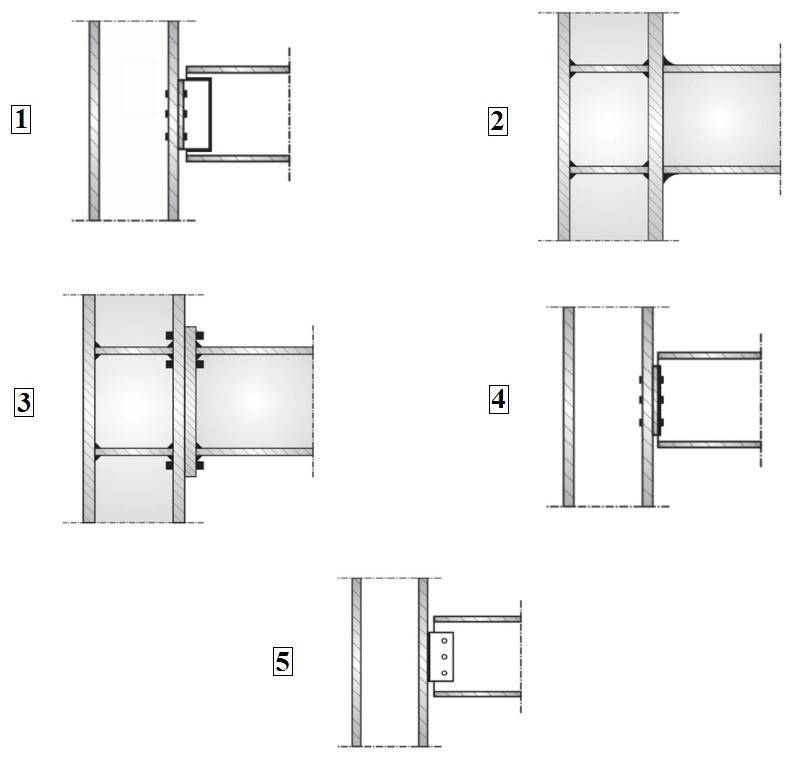
Fonte (adaptado): FAKURY, Ricardo H.; SILVA, Ana L. R. C.; CALDAS, Rodrigo B. Dimensionamento básico de elementos estruturais de aço e mistos de aço e concreto. São Paulo: Pearson Education do Brasil, 2016.
Com base nessas informações, classifique as ligações (1, 2, 3, 4 e 5) apresentadas na figura, como rígidas ou flexíveis. Em seguida, marque a opção que apresenta a resposta correta.
Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
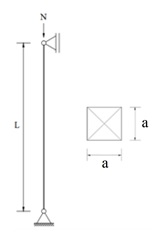
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m
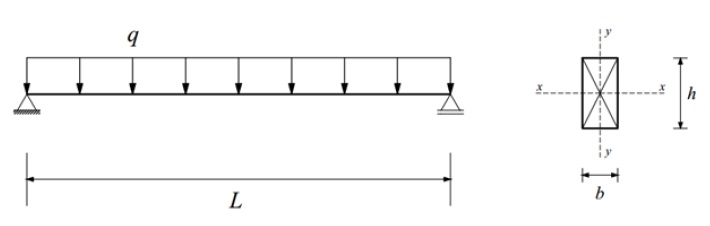
Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.

Rd = 722 kN.
Rd = 767 kN.
Rd = 700 kN.
Rd = 748 kN.
Rd = 793 kN.
Na construção civil brasileira, os principais materiais aplicados com função estrutural são o aço, o concreto e a madeira. Com base nessas informações, e conforme apreciação das propriedades indicadas na tabela abaixo, analise as seguintes afirmativas relacionadas aos três materiais citados:
I. O aço é um material claramente superior à madeira, em diversos aspectos: possui maior durabilidade, maior resistência tanto à tração quanto à compressão, e também é um material naturalmente mais leve.
II. Uma das atribuições do aço quando empregado em estruturas de concreto armado é promover resistência à tração, pois o concreto, em geral, possui baixa resistência à tração.
III. A resistência à compressão do concreto comum geralmente é maior que a resistência à compressão do aço.
IV. A madeira, tanto sujeita à tração quanto à compressão paralela às fibras, possui maior eficiência que o aço e o concreto quando relaciona-se a resistência do material com sua massa específica.

Fonte: PFEIL, Walter; PFEIL, Michèle. Estruturas de madeira: dimensionamento segundo a norma brasileira NBR 7190/97 e critérios das Normas Norte-americanas NDS e Européia EUROCODE 5. Rio de Janeiro: LTC, 2003.
De acordo com a análise efetuada, é possível concluir que as afirmativas CORRETAS são:
I e II
III e IV
II e IV
I e III
I, II e IV
Verificar o diâmetro mínimo, em mm, para a seção transversal circular do tirante de aço MR250 (ASTM A36) ilustrado na figura, sujeito a um esforço normal de tração. No local há elevadas concentrações de pesos fixos. Considerar que o esforço normal de tração é ocasionado pelas seguintes ações:
Peso próprio da estrutura metálica: Ng1 = 32 kN
Peso dos outros componentes não metálicos permanentes: Ng2 = 73 kN
Carga acidental (de ocupação): Nq = 35 kN
Vento: Nv = 20 kN

35 mm.
25 mm.
30 mm.
20 mm.
40 mm.
Determinar o esforço normal resistente de compressão para a coluna soldada (CS) mostrada abaixo, de acordo com a ABNT NBR 8800:2008. As restrições nos dois eixos de análise também são indicadas: a coluna é engastada e livre no eixo X-X, e simplesmente apoiada no eixo Y-Y. Considerar aço MR250 (A36).
Perfil CS 300×62 kg/m:
d = 300 mm
h = 281 mm
tw = 8 mm
tf = 9,5 mm
bf = 300 mm
L = 4000 mm

Nd,res = 1013 kN.
Nd,res = 1447 kN.
Nd,res = 862 kN.
Nd,res = 1976 kN.
Nd,res = 2468 kN.
Em estruturas de aço, as ligações são classificadas conforme o grau de impedimento da rotação relativa das barras conectadas. Na figura abaixo são indicadas algumas ligações de viga e pilar de alma cheia (perfil I ou H) que são frequentemente empregadas na prática, de acordo com a utilização de parafusos e soldas.

Fonte (adaptado): FAKURY, Ricardo H.; SILVA, Ana L. R. C.; CALDAS, Rodrigo B. Dimensionamento básico de elementos estruturais de aço e mistos de aço e concreto. São Paulo: Pearson Education do Brasil, 2016.
Com base nessas informações, classifique as ligações (1, 2, 3, 4 e 5) apresentadas na figura, como rígidas ou flexíveis. Em seguida, marque a opção que apresenta a resposta correta.
Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.

I e II
III e IV
II e IV
I e III
I, II e IV
Verificar o diâmetro mínimo, em mm, para a seção transversal circular do tirante de aço MR250 (ASTM A36) ilustrado na figura, sujeito a um esforço normal de tração. No local há elevadas concentrações de pesos fixos. Considerar que o esforço normal de tração é ocasionado pelas seguintes ações:
Peso próprio da estrutura metálica: Ng1 = 32 kN
Peso dos outros componentes não metálicos permanentes: Ng2 = 73 kN
Carga acidental (de ocupação): Nq = 35 kN
Vento: Nv = 20 kN

35 mm.
25 mm.
30 mm.
20 mm.
40 mm.
Determinar o esforço normal resistente de compressão para a coluna soldada (CS) mostrada abaixo, de acordo com a ABNT NBR 8800:2008. As restrições nos dois eixos de análise também são indicadas: a coluna é engastada e livre no eixo X-X, e simplesmente apoiada no eixo Y-Y. Considerar aço MR250 (A36).
Perfil CS 300×62 kg/m:
d = 300 mm
h = 281 mm
tw = 8 mm
tf = 9,5 mm
bf = 300 mm
L = 4000 mm

Nd,res = 1013 kN.
Nd,res = 1447 kN.
Nd,res = 862 kN.
Nd,res = 1976 kN.
Nd,res = 2468 kN.
Em estruturas de aço, as ligações são classificadas conforme o grau de impedimento da rotação relativa das barras conectadas. Na figura abaixo são indicadas algumas ligações de viga e pilar de alma cheia (perfil I ou H) que são frequentemente empregadas na prática, de acordo com a utilização de parafusos e soldas.

Fonte (adaptado): FAKURY, Ricardo H.; SILVA, Ana L. R. C.; CALDAS, Rodrigo B. Dimensionamento básico de elementos estruturais de aço e mistos de aço e concreto. São Paulo: Pearson Education do Brasil, 2016.
Com base nessas informações, classifique as ligações (1, 2, 3, 4 e 5) apresentadas na figura, como rígidas ou flexíveis. Em seguida, marque a opção que apresenta a resposta correta.
Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.
Peso dos outros componentes não metálicos permanentes: Ng2 = 73 kN
Carga acidental (de ocupação): Nq = 35 kN
Vento: Nv = 20 kN

35 mm.
25 mm.
30 mm.
20 mm.
40 mm.
Determinar o esforço normal resistente de compressão para a coluna soldada (CS) mostrada abaixo, de acordo com a ABNT NBR 8800:2008. As restrições nos dois eixos de análise também são indicadas: a coluna é engastada e livre no eixo X-X, e simplesmente apoiada no eixo Y-Y. Considerar aço MR250 (A36).
Perfil CS 300×62 kg/m:
d = 300 mm
h = 281 mm
tw = 8 mm
tf = 9,5 mm
bf = 300 mm
L = 4000 mm

Nd,res = 1013 kN.
Nd,res = 1447 kN.
Nd,res = 862 kN.
Nd,res = 1976 kN.
Nd,res = 2468 kN.
Em estruturas de aço, as ligações são classificadas conforme o grau de impedimento da rotação relativa das barras conectadas. Na figura abaixo são indicadas algumas ligações de viga e pilar de alma cheia (perfil I ou H) que são frequentemente empregadas na prática, de acordo com a utilização de parafusos e soldas.

Fonte (adaptado): FAKURY, Ricardo H.; SILVA, Ana L. R. C.; CALDAS, Rodrigo B. Dimensionamento básico de elementos estruturais de aço e mistos de aço e concreto. São Paulo: Pearson Education do Brasil, 2016.
Com base nessas informações, classifique as ligações (1, 2, 3, 4 e 5) apresentadas na figura, como rígidas ou flexíveis. Em seguida, marque a opção que apresenta a resposta correta.
Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.

Nd,res = 1013 kN.
Nd,res = 1447 kN.
Nd,res = 862 kN.
Nd,res = 1976 kN.
Nd,res = 2468 kN.
Em estruturas de aço, as ligações são classificadas conforme o grau de impedimento da rotação relativa das barras conectadas. Na figura abaixo são indicadas algumas ligações de viga e pilar de alma cheia (perfil I ou H) que são frequentemente empregadas na prática, de acordo com a utilização de parafusos e soldas.

Fonte (adaptado): FAKURY, Ricardo H.; SILVA, Ana L. R. C.; CALDAS, Rodrigo B. Dimensionamento básico de elementos estruturais de aço e mistos de aço e concreto. São Paulo: Pearson Education do Brasil, 2016.
Com base nessas informações, classifique as ligações (1, 2, 3, 4 e 5) apresentadas na figura, como rígidas ou flexíveis. Em seguida, marque a opção que apresenta a resposta correta.
Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.

Ligação flexível: 5; Ligações rígidas: 1, 2, 3 e 4.
Ligação flexível: 2; Ligações rígidas: 1, 3, 4 e 5.
Ligações flexíveis: 2 e 3; Ligações rígidas: 1, 4 e 5.
Ligações flexíveis: 1, 4 e 5; Ligações rígidas: 2 e 3.
Ligações flexíveis: 1, 3, 4 e 5; Ligação rígida: 2.
Para a ABNT NBR 8800:2008, o valor do coeficiente de ponderação de ação permanente do tipo peso próprio de estruturas metálicas, segundo combinações normais desfavoráveis quanto ao Estado Limite Último, equivale a:
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.
1,10
1,00
1,15
1,40
1,25
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 12 cm. A barra possui comprimento (L) de 330 cm. Considerar madeira conífera serrada de 2ª categoria, classe de resistência C20, classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 30,7 kN.
Fe = 21,44 kN.
Fe = 70,6 kN.
Realizar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 19 kN
Carga acidental (de uso e ocupação): Q1 = 17 kN
Ação do vento de sobrepressão: Qv1 = 12 kN
Ação do vento de sucção: Qv2 = -7 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.
73,9 kN
62,9 kN
70,3 kN
77,6 kN
59,3 kN
Determinar a resistência de cálculo no estado limite último da madeira Pinus elliottii (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 40,4 MPa
Ec0,m = 11 889 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 9,0 MPa; Ec0,ef = 5326,3 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
A viga biapoiada de madeira dicotiledônea indicada na figura abaixo suporta um carregamento uniformemente distribuído ao longo do vão. A viga possui vão entre apoios (L) de 3,3 m e seção transversal retangular 6×16 (cm). Considera-se, nesse caso, classe de carregamento de longa duração, classe de resistência C40 para a madeira, classe 4 de umidade e madeira serrada de 2ª categoria. Na construção não há predominância de pesos de equipamentos fixos, nem de elevadas concentrações de pessoas. O carregamento vertical uniformemente distribuído (q), atuante na viga, ocorre conforme os seguintes valores característicos para as ações:
Peso próprio + demais pesos fixos: qg,k = 3,5 kN/m (grande variabilidade)
Sobrecarga (carga acidental): qq,k = 2,5 kN/m

Com base nessas informações, determine o momento fletor máximo que ocorre na viga (valor de cálculo), em kN.cm. Em caso de resposta decimal, considerar uma casa após a vírgula.
Sobrecarga (carga acidental): qq,k = 2,5 kN/m
